Giải bài 1 2 3 4 5 6 7 8 trang 104 105 sgk Hình học 11

Thuan Nguyen2 ngày ago

1 11 minutes read

Hướng dẫn giải Bài §3. Đường thẳng vuông góc với mặt phẳng, Chương III. Vectơ trong không gian. Quan hệ vuông góc trong không gian, sách giáo khoa Hình học 11. Nội dung bài giải bài 1 2 3 4 5 6 7 8 trang 104 105 sgk Hình học 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập hình học có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.

Lý thuyết

1. Định nghĩa

Đường thẳng $a$ được gọi là vuông góc với mặt phẳng ((alpha)) nếu a vuông góc với mọi đường thẳng $a$ nằm trong mặt phẳng ((alpha)).

Kí hiệu: (a bot left ( alpha right ))

Ta có: (a bot mp(alpha) Leftrightarrow a bot c,forall c subset (alpha))

2. Điều kiện để đường thẳng vuông góc với mặt phẳng

Định lí: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.

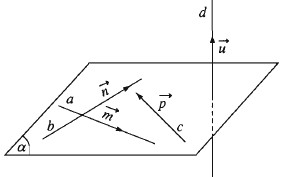
Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh thứ ba của tam giác đó.

3. Tính chất

Tính chất 1: Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Tính chất 2: Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng

Tính chất 1: Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

(left. begin{array}{l} a//b left( alpha right) bot a end{array} right} Rightarrow left( alpha right) bot b)

Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

(left. begin{array}{l} a bot (alpha ) b bot (alpha ) a ne b end{array} right} Rightarrow a//b)

Tính chất 2: Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.

(left. begin{array}{l} a bot (alpha ) left( alpha right)//left( beta right) end{array} right} Rightarrow left( alpha right) bot left( beta right))

Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

(left. begin{array}{l} a bot (alpha ) a bot left( beta right) left( alpha right) ne left( beta right) end{array} right} Rightarrow left( alpha right)//left( beta right))

Tính chất 3: Cho đường thẳng a và mặt phẳng (left ( alpha right )) song song với nhau. Đường thẳng nào vuông góc với (left ( alpha right )) thì cũng vuông góc với a.

(left. begin{array}{l} a//(alpha ) b bot left( alpha right) end{array} right} Rightarrow b bot a)

Nếu một đường thẳng và một mặt phẳng cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.

(left. begin{array}{l} a bot b b bot left( alpha right) a notsubset left( alpha right) end{array} right} Rightarrow a//left( alpha right))

5. Phép chiếu vuông góc và định lí ba đường vuông góc

Định nghĩa: Phép chiếu song song lên mặt phẳng (P) theo phương l vuông góc với mặt phẳng (P) gọi là phép chiếu vuông góc lên mặt phẳng (P).

Định lí ba đường vuông góc: Cho đường thẳng d nằm trong mặt phẳng (left ( alpha right )) và b là đường thẳng không thuộc (left ( alpha right )) đồng thời không vuông góc với (left ( alpha right )). Gọi b’ là hình chiếu vuông góc của b trên (left ( alpha right )). Kho đó a vuông góc với b khi và chỉ khi a vuông góc với b’.

6. Góc giữa đường thẳng và mặt phẳng

Góc giữa đường thẳng d không vuông góc với mặt phẳng (left ( alpha right )) là góc giữa d và hình chiếu d’ của nó trên mặt phẳng (left ( alpha right )).

Đặc biệt: Nếu d vuông góc với mặt phẳng (left ( alpha right )) thì ta nói rằng góc giữa đường thẳng d và mặt phẳng (left ( alpha right )) là 900.

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong mục hoạt động của học sinh trên lớp sgk Hình học 11.

Câu hỏi

1. Trả lời câu hỏi 1 trang 100 sgk Hình học 11

Muốn chứng minh đường thẳng $d$ vuông góc với một mặt phẳng $(α)$, người ta phải làm như thế nào?

Trả lời:

Muốn chứng minh đường thẳng $d$ vuông góc với một mặt phẳng $(α)$, người ta phải chứng minh $d$ vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng $(α)$.

2. Trả lời câu hỏi 2 trang 100 sgk Hình học 11

Cho hai đường thẳng $a$ và $b$ song song với nhau. Một đường thẳng $d$ vuông góc với $a$ và $b$. Khi đó đường thẳng $d$ có vuông góc với mặt phẳng xác định bởi hai đường thẳng song song $a$ và $b$ không ?

Trả lời:

Không vì trái với định lí ($a // b$ thì $a$ và $b$ không cắt nhau)

Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 7 8 trang 104 105 sgk Hình học 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập hình học 11 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 8 trang 104 105 sgk Hình học 11 của Bài §3. Đường thẳng vuông góc với mặt phẳng trong Chương III. Vectơ trong không gian. Quan hệ vuông góc trong không gian trong mặt phẳng cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 7 8 trang 104 105 sgk Hình học 11

1. Giải bài 1 trang 104 sgk Hình học 11

Cho hai đường thẳng phân biệt (a,b) và mặt phẳng ((alpha)). Các mệnh đề sau đây đúng hay sai?

a) Nếu (a//(alpha)) và (bbot (alpha)) thì (abot b).

b) Nếu (a//(alpha)) và (bbot a) thì (bbot (alpha)).

c) Nếu (a//(alpha)) và (b// (alpha)) thì (b//a).

d) Nếu (abot (alpha)) và (bbot a) thì (b// (alpha)).

Bài giải:

a) Đúng (theo tính chất).

b) Sai. Vì thiếu điều kiện: Muốn (bbot (alpha)) thì $b$ cần vuông góc với $2$ đường thẳng cắt nhau trong $(alpha )$.

c) Sai. Vì $a$ và $b$ có thể chéo nhau hoặc cắt nhau.

d) Sai. Vì $b$ có thể nằm trong $(alpha )$.

2. Giải bài 2 trang 104 sgk Hình học 11

Cho tứ diện $ABCD$ có hai mặt $ABC$ và $BCD$ là hai tam giác cân có chung đáy $BC$. Gọi $I$ là trung điểm của cạnh $BC$.

a) Chứng minh rằng $BC$ vuông góc với mặt phẳng $(ADI)$

b) Gọi $AH$ là đường cao của tam giác $ADI$, chứng minh rằng $AH$ vuông góc với mặt phẳng $(BCD).$

Bài giải:

a) Tam giác (ABC) cân tại (A) nên ta có đường trung tuyến ứng với cạnh đáy đồng thời là đường cao do đó: (AIbot BC)

Tương tự ta có: (DIbot BC)

Ta có:

(left. matrix{ AI bot BC hfill cr DI bot BC hfill cr AI cap DI = {rm{{ }}I{rm{} }} hfill cr} right} Rightarrow BC bot (ADI))

b) Ta có (AH) là đường cao của tam giác (ADI) nên (AHbot DI)

Mặt khác: (BCbot (ADI)) mà (AHsubset (ADI)) nên (AHbot BC)

Ta có

(left. matrix{ AH bot BC hfill cr AH bot DI hfill cr BC cap DI = {rm{{ }}I{rm{} }} hfill cr} right} Rightarrow AH bot (BCD))

3. Giải bài 3 trang 104 sgk Hình học 11

Cho hình chóp (S.ABCD) có đáy là hình thoi (ABCD) và có (SA=SB=SC=SD).Gọi (O) là giao điểm của (AC) và (BD). Chứng minh rằng:

a) Đường thẳng (SO) vuông góc với mặt phẳng ((ABCD));

b) Đường thẳng ( AC) vuông góc với mặt phẳng ((SBD)) và đường thẳng (BD) vuông góc với mặt phẳng (SAC).

Bài giải:

a) Theo giả thiết (SA=SC) nên tam giác (SAC) cân tại (S)

Có: (O) là giao của hai đường chéo hình bình hành nên (O) là trung điểm của (AC) và (BD).

Do đó (SO) vừa là trung tuyến đồng thời là đường cao trong tam giác (SAC)

⇒ (SObot AC) (1)

Chứng minh tương tự ta được: (SObot BD) (2)

Từ (1) và (2) ta có:

$left.begin{matrix} SO& perp AC SO& perp BD AC& cap BD end{matrix}right}Rightarrow SOperp (ABCD)$

b) (ABCD) là hình thoi có $AC,BD$ là hai đường chéo nên (ACbot BD) (Tính chất hình bình hành) (3)

Từ (1) và (3) ta có:

$left.begin{matrix} SO& perp AC AC& perp BD SO& cap BD end{matrix}right}Rightarrow ACperp (SBD)$

Từ (2) và (3) ta có:

$left.begin{matrix} SO& perp BD AC& perp BD SO& cap AC end{matrix}right}Rightarrow BDperp (SAC)$

4. Giải bài 4 trang 105 sgk Hình học 11

Cho tứ diện (OABC) có ba cạnh (OA, OB, OC) đôi một vuông góc. Gọi (H) là chân đường vuông góc hạ từ (O) tới mặt phẳng ((ABC)). Chứng minh rằng:

a) $H$ là trực tâm của tam giác (ABC);

b) (frac{1}{OH^{2}}=frac{1}{OA^{2}}+frac{1}{OB^{2}}+frac{1}{OC^{2}}.)

Bài giải:

Kéo dài $AH$ cắt $BC$ tại $E, CH$ cắt $AB$ tại $K.$

a) Chứng minh $H$ là trực tâm tam giác ABC.

(H) là hình chiếu của (O) trên mp ((ABC)) (gt) nên (OH ⊥ (ABC) Rightarrow OH ⊥ BC) (Tính chất)

Mặt khác: (OA ⊥ OB), (OA ⊥ OC) (gt) mà $OB cap OC$

(Rightarrow OA ⊥ (OBC) Rightarrow OA ⊥ BC) (Tính chất)

Ta có:

$left.begin{matrix} OH& perp BC OA& perp BC OH& cap OA end{matrix}right}Rightarrow BCperp (OAH)$

mà: (AHsubset (OAH) Rightarrow BC ⊥ AH) (1)

Chứng minh tương tự: (OA ⊥ OC), (OB ⊥ OC) (gt) mà $OA cap OB$

(Rightarrow OC ⊥ (OAB) Rightarrow OC ⊥ AB) (Tính chất)

Ta có:

$left.begin{matrix} OH& perp AB OC& perp AB OH& cap OC end{matrix}right}Rightarrow ABperp (OHC)$

mà: (CHsubset (OHC) Rightarrow AB ⊥ HC) (2)

Từ (1) (2) (Rightarrow H) là trực tâm của tam giác (ABC).

b) Chứng minh: (frac{1}{OH^{2}}=frac{1}{OA^{2}}+frac{1}{OB^{2}}+frac{1}{OC^{2}})

Trong mặt phẳng ((ABC)) vì (E = AH ∩ BC), (OH ⊥ (ABC)), (AE ⊂ (ABC) Rightarrow OH ⊥ AE) tại (H); (OA ⊥ (ABC), OE ⊂ (ABC) Rightarrow OA ⊥ OE)

⇒ (OH) là đường cao của tam giác vuông (OAE)

⇒ (frac{1}{OH^{2}}=frac{1}{OA^{2}}+frac{1}{OE^{2}}) (3)

Mặt khác (OE) là đường cao của tam giác vuông (OBC)

⇒ (frac{1}{OE^{2}}=frac{1}{OB^{2}}+frac{1}{OC^{2}})

Thay vào (3) ta có:

(frac{1}{OH^{2}}=frac{1}{OA^{2}}+frac{1}{OE^{2}} =frac{1}{OA^{2}}+frac{1}{OB^{2}}+frac{1}{OC^{2}}.)

5. Giải bài 5 trang 105 sgk Hình học 11

Trên mặt phẳng ((α)) cho hình bình hành (ABCD). Gọi (O) là giao điểm của (AC) và (BD). (S) là một điểm nằm ngoài mặt phẳng ((α)) sao cho (SA = SC, SB = SD). Chứng minh rằng:

a) (SO ⊥ (α));

b) Nếu trong mặt phẳng ((SAB)) kẻ (SH) vuông góc với (AB) tại (H) thì (AB) vuông góc mặt phẳng ((SOH)).

Bài giải:

a) Theo giả thiết: (SA = SC) nên tam giác (SAC) cân tại (S).

Lại có: (O) là trung điểm của (AC) nên (SO) là đường trung tuyến đồng thời là đường cao của tam giác cân $SAC$ nên (SObot AC)

Chứng minh tương tự với $SB=SD$, $O$ là trung điểm của $BD$ ta có: (SObot BD)

Ta có:

$$left. matrix{ SO bot BD hfill cr SO bot AC hfill cr BD cap AC = {rm{{ O} }} hfill cr} right} Rightarrow SO bot (ABCD)$$

Hay (SO ⊥ mp(α)) (đpcm).

b) (SO ⊥ (ABCD) Rightarrow SO ⊥ AB) (1)

Mà (SH ⊥ AB) (gt) (2)

Từ (1) và (2) ta có;

$$left. matrix{ SO bot AB hfill cr SH bot AB hfill cr SO cap SH = {rm{{ S} }} hfill cr} right} Rightarrow AB bot (SHO)$$

6. Giải bài 6 trang 105 sgk Hình học 11

Cho hình chóp (S.ABCD) có đáy là hình thoi (ABCD) và có cạnh (SA) vuông góc với mặt phẳng ((ABCD)). Gọi (I) và (K) là hai điểm lần lượt lấy trên hai cạnh (SB) và (SD) sao cho (frac{SI}{SB}=frac{SK}{SD}.) Chứng minh:

a) (BD) vuông góc với (SC);

b) (IK) vuông góc với mặt phẳng ((SAC)).

Bài giải:

a) Ta có: $BDperp AC$ (tính chất đường chéo hình thoi)

Lại có: $SAperp (ABCD)$ (gt)

$BDsubset (ABCD)Rightarrow BDperp SA$

Ta có: $left.begin{matrix} BD& perp AC BD& perp SA AC& cap SA end{matrix}right}Rightarrow BDperp (SAC)$

mà $SCsubset (SAC)Rightarrow BDperp SC$.

b) Theo giả thiết (frac{SI}{SB}=frac{SK}{SD}) theo định lí Ta-lét ta có (IK//BD)

Từ chứng minh câu a) ta có:

$BDperp (SAC)$ $Rightarrow IKperp (SAC)$

7. Giải bài 7 trang 105 sgk Hình học 11

Cho tứ diện (SABC) có cạnh (SA) vuông góc với mặt phẳng ((ABC)) và có tam giác (ABC) vuông tại (B). Trong mặt phẳng ((SAB)) kẻ từ (AM) vuông góc với (SB) tại (M). Trên cạnh (SC) lấy điểm (N) sao cho (frac{SM}{SB}=frac{SN}{SC}.) Chứng minh rằng:

a) (BC ⊥ (SAB)) và (AM ⊥ (SBC));

b) (SB ⊥ AN).

Bài giải:

a) Chứng minh: $BCperp (SAB)$

Theo giả thiết: $SA perp (ABC)$ mà $BCsubset (ABC)Rightarrow SAperp BC$

Tam giác ABC vuông tại B nên $ABperp BC$

Vậy: $left.begin{matrix} SA& perp BC AB& perp BC SA& cap AB end{matrix}right}Rightarrow BCperp (SAB)$

Chứng minh: $AMperp (SBC)$

Ta có: $AMsubset (SAB),BCperp (SAB)Rightarrow BCperp AM$

Vậy: $left.begin{matrix} AM& perp BC (cmt) AM& perp SB (gt) BC& cap SB end{matrix}right}Rightarrow AMperp (SBC)$

b) Theo giả thiết: (AM ⊥ (SBC)) nên (AMbot SB)

Giả thiết (frac{SM}{SB}=frac{SN}{SC}) nên theo định lí Ta – lét ta có: (MN// BC)

Mà (BCbot SB) (do (BCbot (SAB))) do đó (MNbot SB)

Vậy:

$left.begin{matrix} MN& perp SB (cmt) AM& perp SB (cmt) AM& cap MN end{matrix}right}Rightarrow SBperp (AMN)Rightarrow SBperp MN$

8. Giải bài 8 trang 105 sgk Hình học 11

Cho điểm (S) không thuộc cùng mặt phẳng ((α)) có hình chiếu là điểm (H). Với điểm (M) bất kì trên ((α)) và (M) không trùng với (H), ta gọi (SM) là đường xiên và đoạn (HM) là hình chiếu của đường xiên đó. Chứng minh rằng:

a) Hai đường thẳng xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau;

b) Với hai đường xiên cho trước, đường xiên nào lớn hơn thì có hình chiếu lớn hơn và ngược lại đường xiên nào có hình chiếu lớn hơn thì lớn hơn.

Bài giải:

Gọi (SN) là một đường xiên khác.

a) Xét hai tam giác vuông (SHM) và (SHN) có (SH) cạnh chung.

Nếu (SM = SN Rightarrow ∆SHM = ∆SHN (c-g-c))

(Rightarrow HM = HN).(2 cạnh tương ứng)

Ngược lại nếu (HM = HN) thì (∆SHM = ∆SHN (c-g-c))

(Rightarrow SM = SN). (2 cạnh tương ứng)

Vậy: Hai đường thẳng xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau.

b) Xét tam giác vuông (SHM) và (SHN) có (SH) cạnh chung.

Giả sử (SN > SM)