Bài 58 trang 83 sgk toán lớp 7- tập 2
Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ngoài tam giác.
Hướng dẫn:
Trực tâm của tam giác vuông trùng với đỉnh góc vuông là vì mỗi cạnh góc vuông của tam giác chính là đường cao cua tam giác nên 2 cạnh góc vuông và đường cao ứng với cạnh huyền trong tam giác vuông cắt nhau tại đỉnh góc vuông.
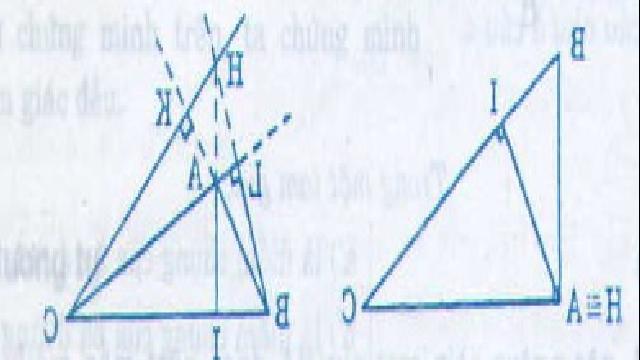
+ Nếu tam giác ABC có góc A tù => BC là cạnh lớn nhất
=> BC > BA
Kẻ đường cao BL thì LA; LC là hai hình chiếu của BA, BC => LA < LC
=> A nằm giữa L và C tức đường cao BL nằm ngoài tam giác ABC
Tương tự đường cao CK nằm ngoài tam giác ABC
Nên điểm cắt nhau của ba đường cao nằm ngoài tam giác
Bài 59 trang 83 sgk toán lớp 7- tập 2
59. Cho hình dưới
a) Chứng minh NS ⊥ LM
b) Khi (widehat{LNP}) =500, hãy tính góc MSP và góc PSQ
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có (widehat{LNP}) =500 nên (widehat{QMN}) =400
∆MPS vuông tại Q có (widehat{QMP}) =400 nên (widehat{MSP}) =500
Suy ra (widehat{PSQ}) =1300(kề bù)
Bài 60 trang 83 sgk toán lớp 7- tập 2
Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K)
Kẻ đường thẳng l vuông góc với d tại J, trên l lấy điểm M khác với điểm J. đường thẳng qua l vuông góc với MK cắt l tại N. chứng minh rằng KN ⊥ IM.
Giải:
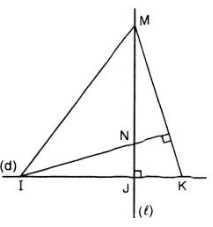
Nối M với I ta được ΔMIK.
Trong ΔMIK có: MJ ⊥ IK (do l ⊥ d) và IN ⊥ MK
Do đó N là trực tâm của ΔMIK.
Suy ra KN là đường cao thứ ba của ΔMIK hay KN ⊥ IM (đpcm).
Bài 61 trang 83 sgk toán lớp 7- tập 2
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ta trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB, HAC
Hướng dẫn:
Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E
a) ∆HBC có:
HN ⊥ BC nên HN là đường cao
BE ⊥ HC nên BE là đường cao
CM ⊥ BH nên CM là đường cao
Vậy A là trực tâm của ∆HBC
b) Tương tự trực tâm của ∆AHB là C, ∆AHC là B
Bài 62 trang 83 sgk toán lớp 7- tập 2
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Hướng dẫn:
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> (widehat{FBC}= widehat{ECB})
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.
Giaibaitap.me
