Toán 12: Đề kiểm tra học kì 2 dạng trắc nghiệm (Đề 4)
Câu 1: Cho $int_{0}^{1}f(x)dx$ = 1 và $int_{1}^{2}f(2x-1)dx$ = 6. Tính tích phân $int_{0}^{3}f(x)dx$ bằng:
- A. 7
- B. 5
-
C. 13
- D. 4
Câu 2: Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ dưới đây:
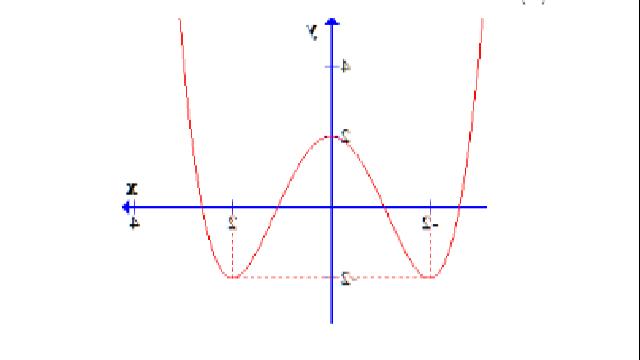
Số nghiệm thực của phương trình 4|f(x)| – 5 = 0 là:
-
A. 8
- B. 4
- C. 7
- D. 6
Câu 3: Tính đạo hàm của hàm số y = $log_{2}$(3x+1):
- A. y’ = $frac{1}{(3x+1)ln2}$
- B. y’ = $frac{3}{3x+1}$
- C. y’ = $frac{1}{3x+1}$
-
D. y’ = $frac{3}{(3x+1)ln2}$
Câu 4: Tìm nghiệm của phương trình $log_{2}(1-x)$ = 2
-
A. x = -3
- B. x = -4
- C. x = 3
- D. x = 5
Câu 5: Gọi (H) là hình phẳng giới hạn bởi các đường y = x-2; y = 0; x = -3; x = 4. Thể tích của khối tròn xoay khi cho (H) quay quanh trục Ox bằng:
- A. $frac{21pi }{2}$
- B. $frac{29pi }{2}$
-
C. $frac{133pi }{3}$
- D. 7$pi $
Câu 6: Cho phương trình $5^{x}+m=log_{5}(x-m)$ với m là tham số. Có bao nhiêu giá trị nguyên của m $in $ (-20;20) để phương trình đã cho có nghiệm?
- A. 20
-
B. 19
- C. 9
- D. 21
Câu 7: Số phức có phần thực bằng 3 và phần ảo bằng -4 là:
- A. 3+4i
-
B. 3-4i
- C. 4-3i
- D. 4+3i
Câu 8: Cho hàm số y = $ax^{4}+bx^{2}+c$ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
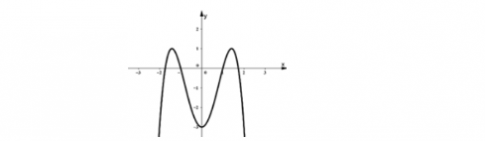
- A. a>0, b<0, c<0
- B. a<0, b<0, c<0
-
C. a<0, b>0, c<0
- D. a>0, b<0, c>0
Câu 9: Cho hàm số f(x) liên tục trên R. Gọi S là diện tích hình phẳng giới hạn bởi các đường y=f(x), y=0, x=-1, x=2 (như hình vẽ). Mệnh để nào dưới đây đúng?
-
A. S = $int_{-1}^{1}f(x)dx – int_{1}^{2}f(x)dx$
- B. S = $int_{-1}^{1}f(x)dx + int_{1}^{2}f(x)dx$
- C. S = $int_{-1}^{2}f(x)dx$
- D. S = -$int_{-1}^{2}f(x)dx$
Câu 10: Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình vẽ.
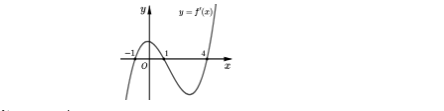
Hàm số y = f($x^{2}$) nghịch biến trên khoảng:
-
A. (-1;10)
- B. (-2;-1)
- C. (1;4)
- D. (0;1)
Câu 11: Trong không gian Oxyz, cho mặt cầu (S): $x^{2}+y^{2}+z^{2}-2x-4y-4z-16=0$. Bán kính của mặt cầu (S) là:
-
A. 5
- B. 4
- C. $2sqrt{5}$
- D. $sqrt{52}$
Câu 12: Cho khối chóp S.ABCD có thể tích bằng $2a^{3}$, đáy ABCD là hình thang với đáy lớn là AB và AB = 3CD. Gọi M là trung điểm cạnh SA, N là điểm thuộc cạnh CB sao cho BN = 3NC. Mặt phẳng (DMN) cắt cạnh SB tại I. Tính thể tích khối chóp AMDNI.
- A. $frac{3a^{3}}{8}$
- B. $frac{5a^{3}}{8}$
- C. $frac{10a^{3}}{12}$
-
D. $frac{3a^{3}}{4}$
Câu 13: Cho ba số dương a, b, c ($aneq 1; bneq 1$) và số thực $alpha neq 0$. Đẳng thức nào sau đây là sai?
-
A. $log_{b}c = frac{log_{a}c}{log_{a}b}$
- B. $log_{a}bc = log_{a}b+log_{a}c$
- C. $log_{a}frac{b}{c} = log_{a}b-log_{a}c$
- D. $log_{a}b^{alpha }=frac{1}{alpha }log_{a}b$
Câu 14: Đồ thị hàm số y = $frac{x-3}{x^{2}-9}$ có mấy đường tiệm cận:
- A. 0
- B. 3
- C. 1
-
D. 2
Câu 15: Cho hàm số y = $x^{3}-3x^{2}+x$ có đồ thị (C). Phương trình tiếp tuyến của (C) có hệ số góc nhỏ nhất là:
- A. y = -x
- B. y = -2x+3
-
C. y = -2x+1
- D. y = x
Câu 16: Số phức liên hợp của số phức z = -1+2i là:
- A. 2+i
- B. 1+2i
-
C. -1-2i
- D. 1-2i
Câu 17: Hàm số y = $frac{2x+3}{x+1}$ có bao nhiêu điểm cực trị?
- A. 3
- B. 1
- C. 2
-
D. 0
Câu 18: Tập nghiệm của bất phương trình $log_{frac{1}{2}}(2x-1)>-1$ là:
-
A. $(frac{1}{2};frac{3}{2})$
- B. $(frac{3}{2};+infty )$
- C. $(1;frac{3}{2})$
- D. $(-infty ;frac{3}{2})$
Câu 19: Trong không gian Oxyz, cho đường thẳng d: $frac{x-1}{2}=frac{y-2}{3}=frac{z+2}{-1}$. Điểm nào dưới đây thuộc đường thẳng d:
- A. (5;1;-4)
- B. (-1;-1;1)
-
C. (3;5;-3)
- D. (1;2;2)
Câu 20: Cho x, y thuộc R thỏa mãn x+3y+(2x-y)i=13+5i. Giá trị của biểu thức $x^{2}-y^{2}$ bằng:
- A. 10
-
B. 7
- C. 25
- D. 5
Câu 21: Trong không gian Oxyz, cho mặt phẳng (P) có phương trình 2x-3y+z+4=0. Vecto nào dưới đây là một vecto pháp tuyến của mặt phẳng (P):
- A. (-2;3;4)
- B. (2;-3;4)
- C. (2;-3;0)
-
D. (2;-3;1)
Câu 22: Rút gọn biểu thức P = $(5-2sqrt{6})^{2020}.(5+2sqrt{6})^{2020}$ được kết quả bằng:
- A. 1
- B. 2
- C. 49 + 20$sqrt{6}$
-
D. 49 – 20$sqrt{6}$
Câu 23: Thể tích của khối trụ có chiều cao bằng h và diện tích đáy bằng B là:
-
A. V = Bh
- B. V = $frac{1}{4}$Bh
- C. V = $frac{1}{3}$Bh
- D. V = $frac{1}{2}$Bh
Câu 24: Cho hình chóp S.ABC. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Tỉ số thể tích $frac{V_{S.ABC}}{V_{S.MNP}}$ bằng:
- A. 2
-
B. 8
- C. 12
- D. 3
Câu 25: Tích các nghiệm của phương trình $2^{2x^{2}-5x-1} = frac{1}{2}$ là:
- A. 2
-
B. 0
- C. -2
- D. $frac{5}{2}$
Câu 26: Cho hàm số f(x) có đạo hàm f'(x) = $x(x-1)^{2}(x+4)^{8}$ với mọi x thuộc R. Số điểm cực trị của hàm số đã cho là:
- A. 6
- B. 1
- C. 3
-
D. 2
Câu 27: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB = a, AD = a$sqrt{3}$, SA vuông góc với mặt phẳng đáy và SC tạo với đáy một góc $60^{circ}$. Thể tích của khối chóp S.ABCD bằng:
-
A. 2$a^{3}$
- B. $a^{3}sqrt{3}$
- C. $frac{a^{3}sqrt{3}}{3}$
- D. 6$a^{3}$
Câu 28: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
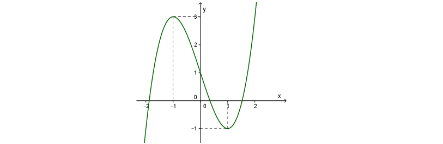
- A. y = $x^{3}+3x+1$
- B. y = $frac{-1}{3}x^{3}+x+1$
- C. y = $x^{4}-2x^{2}+1$
-
D. y = $x^{3}-3x+1$
Câu 29: Cho khối lập phương có cạnh bằng 4. Thể tích của khối lập phương đã cho bằng:
-
A. 64
- B. 12
- C. 16
- D. 4
Câu 30: Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình dưới:
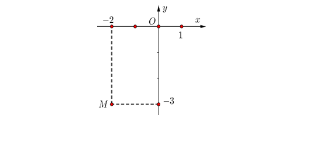
- A. (1+i)(2-i)
- B. (1+i)(2-3i)
-
C. $frac{3-2i}{i}$
- D. $frac{i}{2+3i}$
Câu 31: Cho $z_{1}, z_{2}$ là hai nghiệm phức của phương trình $z^{2}-2z+4=0$. Giá trị của biểu thức 3|$z_{1}$| – |$z_{2}$| bằng:
- A. 2$sqrt{3}$
- B. 6
- C. 4$sqrt{3}$
-
D. 4
Câu 32: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $Delta _{1}: frac{x+1}{1} = frac{y-2}{2} = frac{z+1}{3}$ và $Delta _{2}: frac{x+1}{1} = frac{y-2}{2} = frac{z+1}{-3}$. Đường thẳng d đi qua điểm (1;1;3) và vuông góc với cả hai đường thẳng $Delta _{1}, Delta _{2}$ có phương trình là:
- A. $left{begin{matrix}x=1+t y=1+t z=3+3tend{matrix}right.$
-
B. $left{begin{matrix}x=1+2t y=1-t z=3end{matrix}right.$
- C. $left{begin{matrix}x=-12+t y=6+t z=3tend{matrix}right.$
- D. $left{begin{matrix}x=1-2t y=1+t z=3-tend{matrix}right.$
Câu 33: Cho hàm số y = $x^{3}+3x$ có đồ thị (C). Tìm giao điểm của (C) và trục hoành:
- A. 2
- B. 3
- C. 0
-
D. 1
Câu 34: Trong không gian Oxyz, cho hai điểm A(1;-2;1) và B(-1;0;3). Phương trình mặt phẳng trung trực của đoạn AB là:
- A. -x+y+z-6=0
- B. x-y-z+4=0
-
C. x-y-z+1=0
- D. x-y-z-2=0
Câu 35: Tìm giá trị lớn nhất M của hàm số y = $x^{3}+2x^{2}-7x$ trên đoạn [0;4].
-
A. M = 68
- B. M = 13
- C. M = 70
- D. M = -4
Câu 36: Hàm số nào dưới đây đồng biến trên R
-
A. y = $x^{3}+3x$
- B. y = $-x^{2}+x$
- C. y = $frac{x+2}{x+4}$
- D. y = tanx
Câu 37: Cho $int_{1}^{e}frac{sqrt{3+lnx}}{x}dx = frac{a-bsqrt{3}}{3}$ với a, b là các số nguyên. Mệnh đề nào dưới đây đúng?
- A. a – 2b = 12
-
B. a – b = 10
- C. ab = 24
- D. a + b = 10
Câu 38: Cho tứ diện SABC có SA, SB, SC đôi một vuông góc. Biết SA = SB = a; SC = 2a. Tính khoảng cách từ điểm S đến mặt phẳng (ABC)
-
A. $frac{2a}{3}$
- B. $frac{a}{2}$
- C. $frac{asqrt{2}}{2}$
- D. $frac{2asqrt{5}}{5}$
Câu 39: Họ nguyên hàm của hàm số f(x) = 4x – cosx là:
- A. 4 + sinx + C
-
B. $2x^{2}$ – sinx + C
- C. $2x^{2}$ + sinx + C
- D. 4 – sinx + C
Câu 40: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): -x+y+3z-2=0. Phương trình mặt phẳng ($alpha $) đi qua A(2;-1;1) và song song với (P) là:
- A. x-y+3z-6=0
- B. -x+y-3z=0
-
C. -x+y+3z=0
- D. -x-y+3z=0
Câu 41: Trong không gian Oxyz, hình chiếu vuông góc của điểm M(3;-2;1) trên mặt phẳng (Oxz) có tọa độ là:
- A. (0;-2;1)
- B. (0;0;1)
-
C. (3;0;1)
- D. (3;-2;0)
Câu 42: Cho hàm số y = f(x) có bảng biến thiên như sau:
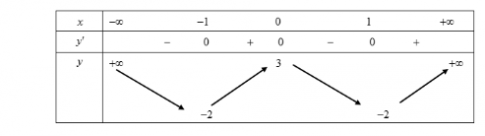
Hàm số đã cho đạt cực đại tại:
- A. x = -2
-
B. x = 0
- C. x = -1
- D. x = 3
Câu 43: Đường thẳng d đi qua điểm M(1;-2;1) và vuông góc với mặt phẳng x-2y+3z-4=0 có phương trình là:
- A. $frac{x-1}{1} = frac{y+2}{2} = frac{z-1}{-3}$
- B. $frac{x+1}{1} = frac{y-2}{-2} = frac{z-1}{3}$
-
C. $frac{x+1}{1} = frac{y-2}{-2} = frac{z+5}{3}$
- D. $frac{x-1}{1} = frac{y+2}{-2} = frac{z+1}{3}$
Câu 44: Cho số phức z thỏa mãn z(1-2i) + $bar{z}$i = 15 + i. Tìm mô đun của số phức z.
- A. |z| = 2$sqrt{5}$
-
B. |z| = 5
- C. |z| = 2$sqrt{3}$
- D. |z| = 4
Câu 45: Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số y = $-x^{3}-mx^{2}+(4m+9)x+5$ nghịch biến trên R.
-
A. 7
- B. 6
- C. 4
- D. 5
Câu 46: Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị như hình vẽ.

Gọi S là tập tất cả các giá trị nguyên của tham số m để phương trình f(sinx) = 2sinx + m có nghiệm trong khoảng (0;$pi $). Tính tổng các giá trị của S.
- A. -5
-
B. -6
- C. 10
- D. -3
Câu 47: Xét tất cả các số dương a và b thỏa mãn $log_{5}a = log_{125}(ab)$.Mệnh đề nào dưới đây đúng?
- A. $a = b^{2}$
- B. $a^{3} = b$
- C. a = b
-
D. $a^{2} = b$
Câu 48: Tập xác định D của hàm số y = $log_{2}(2x-1)$ là:
- A. D = ($-infty ;frac{1}{2}$)
- B. D = (0;$+infty $)
-
C. D = ($frac{1}{2};+infty $)
- D. D = ($frac{-1}{2};+infty $)
Câu 49: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quang của hình nón đỉnh S và đáy là hình tròn nội tiếp ABCD là:
- A. $frac{pi a^{2}sqrt{17}}{6}$
-
B. $frac{pi a^{2}sqrt{17}}{4}$
- C. $frac{pi a^{2}sqrt{17}}{8}$
- D. $frac{pi a^{2}sqrt{15}}{4}$
Câu 50: Cho hàm số f(x) có đạo hàm f'(x) = cosx và f(0) = 1. Giá trị $int_{0}^{pi }f(x)dx$ bằng:
- A. 0
- B. $pi $
- C. 2
-
D. 2 + $pi $
